Phân tích nhiệt được thực hiện bằng cách sử dụng phương pháp phần tử hữu hạn dựa trên phần mềm Midas Civil. Sau đó, phương pháp quy hoạch lập thí nghiệm được sử dụng để thiết lập các hàm toán học cho phép xác định nhiệt độ tối đa và chênh lệch nhiệt độ tối đa trong thân kết cấu bê tông.
Nghiên cứu chỉ ra rằng hàm lượng xi măng đóng vai trò quyết định so với nhiệt độ ban đầu của bê tông trong việc xác định nhiệt độ tối đa và chênh lệch nhiệt độ tối đa. Bên cạnh đó, các hàm toán học thu được đã phản ánh sự ảnh hưởng và tương quan của các thông số đã nêu đến sự thay đổi nhiệt độ và chênh lệch nhiệt độ của kết cấu bê tông khối lớn.
1. Giới thiệu
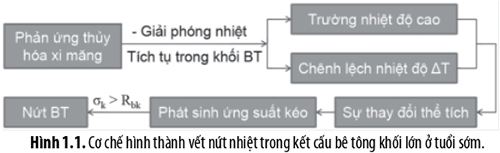
Do nhiệt thủy hóa của xi măng trong kết cấu bê tông khối lớn trong giai đoạn xây dựng, độ dốc nhiệt độ cao giữa môi trường xung quanh và lõi của kết cấu khối được tạo ra khi nhiệt từ khối bê tông không thể tiêu tan nhanh chóng. Kết quả của cơ chế này là các vết nứt hình thành trên bề mặt bê tông do ứng suất nhiệt ở tuổi sớm của bê tông [1]. Hình 1.1 cho thấy cơ học của mặt cắt vết nứt nhiệt gây ra bởi gradien nhiệt độ cao từ quá trình hydrat hóa xi măng.

Nhiệt độ tối đa trong khối bê tông và sự thay đổi nhiệt độ của nó theo thời gian phụ thuộc vào các yếu tố sau [2]:
- Tính chất của hỗn hợp bê tông;
- Yếu tố khí hậu;
- Thời gian thi công;
- Chiều dày các lớp đổ;
- Nhiệt độ ban đầu của hỗn hợp bê tông;
Có một số cách để giảm nhiệt độ cao trong kết cấu bê tông khối lớn, chẳng hạn như giảm hàm lượng xi măng, sử dụng hỗn hợp bê tông sinh nhiệt thấp, làm mát trước bê tông, làm mát sau bê tông bằng cách sử dụng ống làm mát, cách nhiệt bề mặt, hoặc sử dụng bê tông có chứa cốt liệu giãn nở nhiệt thấp.
Bê tông khối lớn có thể bị nứt do ứng suất phát sinh từ sự thay đổi thể tích không đều và bị kìm giữ của khối bê tông [3]. Sự thay đổi thể tích này phát sinh từ các yếu tố như: quá trình co khô, ngót, nở nhiệt của bê tông và độ chênh lệch nhiệt độ ΔT giữa các phần của bê tông. Cơ chế nứt được mô tả tóm tắt ở Hình 1.1.
Ngoài ra, sử dụng phương pháp quy hoạch thực nghiệm để thiết lập mô hình toán học cũng là một phương pháp thích hợp để khống chế nhiệt độ cực đại trong kết cấu bê tông khối lớn. Mô hình toán học được sử dụng để điều chỉnh hợp lý các thông số cấp phối bê tông nhằm khống chế hoàn hảo nhiệt độ cực đại xuất hiện trong bê tông khối lớn [4].
2. Đối tượng và phương pháp nghiên cứu
Đối tượng nghiên cứu
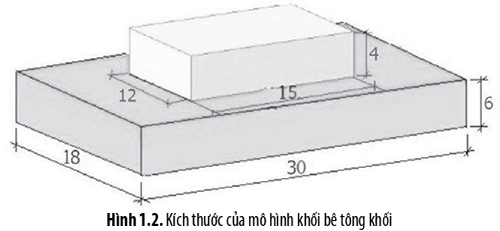
Trong nghiên cứu, một mô hình 3D bao gồm một khối bê tông có kích thước: 12x15x4m đặt trên nền 18x30x6m.
Nhiệt độ xung quanh ảnh hưởng đáng kể đến nhiệt độ tối đa. Nhiệt độ không khí thay đổi theo thời gian được tính theo phương trình sau [5]:
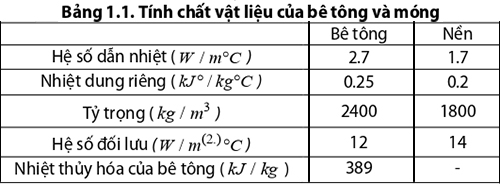
Trong nghiên cứu, nhiệt độ ban đầu của nền được giả định bằng 20°C. Ngoài ra, các tính chất của bê tông và nền được sử dụng làm dữ liệu đầu vào để xác định sự phân bố nhiệt độ trong khối bê tông, được trình bày trong Bảng 1.1 [6-7]
Mô hình toán học phụ thuộc tham số đầu vào của hỗn hợp bê tông
Phương pháp quy hoạch thí nghiệm được sử dụng để xây dựng mô hình toán học. Ảnh hưởng của các thông số đầu vào của hỗn hợp bê tông đến trường nhiệt độ trong bê tông khối lớn được xem xét bằng cách thiết lập hàm mục tiêu. Hàm mục tiêu của mô hình thực nghiệm được biểu diễn bằng giá trị cực đại nhiệt độ Ti ( Tmax, °C) và chênh lệch nhiệt độ cực đại DeltaTi ( DeltaTmax, °C) của bê tông. Đây là hàm toán học phụ thuộc vào hàm lượng xi măng X1 thay đổi trong khoảng 280 - 450kg/m³ và nhiệt độ ban đầu của hỗn hợp bê tông X2, dao động từ 15 - 30°C [11]. Bảng 2 cho thấy mức độ biến thiên của các tham số được sử dụng trong quy hoạch.
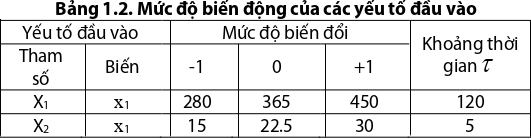
Số lượng thí nghiệm (N) được mô tả lập kế hoạch có thể xác định bởi [12]:
N = 2k + 1 (2)
Trong đó: k - số lượng tham số được xét k=2; 1- Số thí nghiệm tại trung tâm.
Do đó, giá trị của N=5 được thử nghiệm.
Công thức toán học để xác định nhiệt độ cực đại và chênh lệch nhiệt độ cực đại trong khối bê tông có thể được biểu thị bằng đa thức bậc hai như sau:
Phương pháp truyền nhiệt phần tử hữu hạn
Phương trình truyền nhiệt chi phối trong hệ Carte sian toàn cầu có thể được mô tả bằng phương trình Fourier như trong phương trình [8-10]:
Để giải phương trình (4), cần áp dụng phương trình hợp điều kiện biên, như điều kiện Dirichlet, điều kiện biên Neumann, điều kiện biên Robin và điều kiện biên hỗn hợp [8-10].
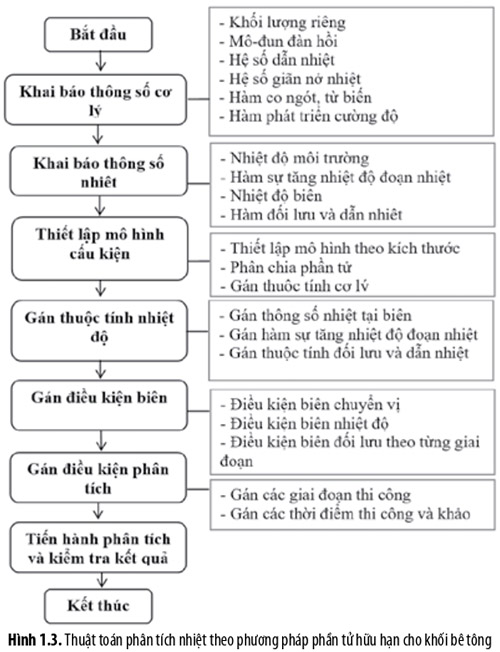
Để giải bài toán truyền nhiệt phức tạp như mô tả trong phương trình (4), phần mềm sử dụng phương pháp phần tử hữu hạn - Midas Civil là một giải pháp phù hợp để phân tích kết cấu nhiệt ứng xử trong khối bê tông [6-7]. Sơ đồ thuật toán cho phân tích nhiệt được giới thiệu trong hình sau.
Vì mô hình có tính đối xứng nên sử dụng một phần tư kích thước mô hình thực tế để sử dụng trong mô hình phần tích theo phương pháp phần tử hữu hạn như trong Hình 1.4. Lưới của mô hình được chia với số lượng 1800 phần tử, tương ứng với 2352 nút, được sử dụng để mô phỏng phân tích.
3. Kết quả và thảo luận
Nhiệt độ tối đa thu được từ phân tích kết quả được thể hiện trong hình 1.5-1.8 và tóm tắt trong Bảng 1.3.
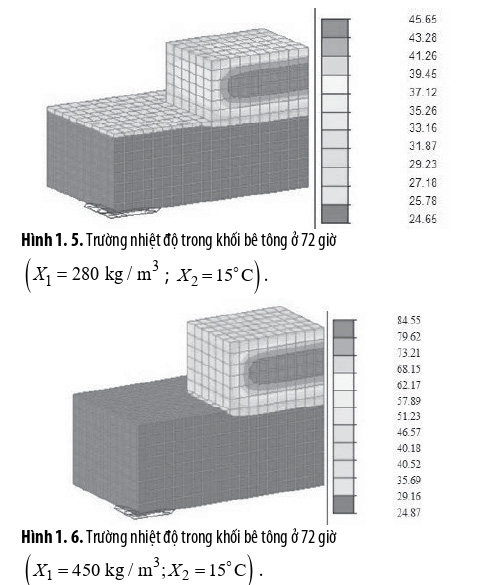
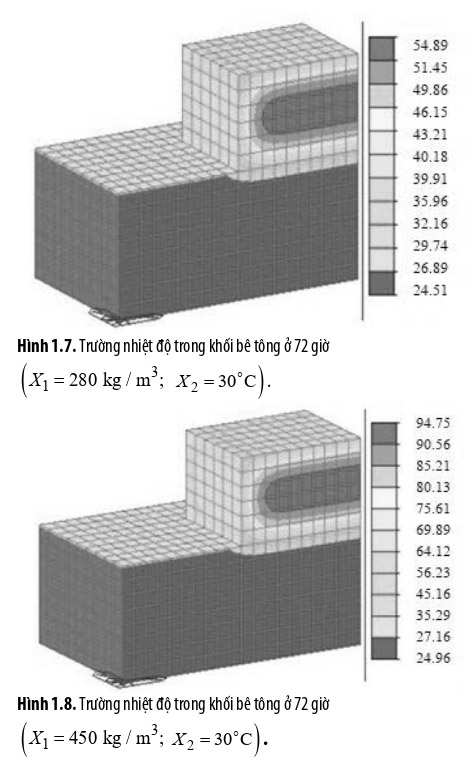
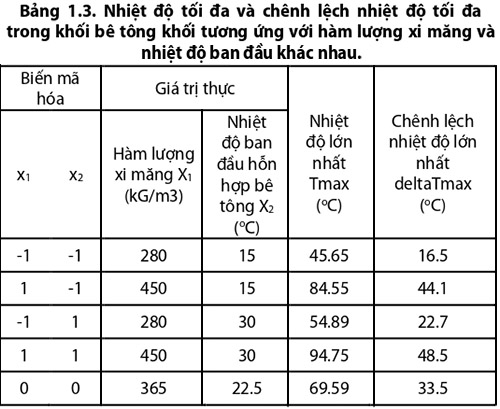
Có thể thấy rằng sự gia tăng hàm lượng xi măng làm tăng nhiệt độ tối đa nhiều hơn so với việc tăng nhiệt độ ban đầu của hỗn hợp bê tông. Như vậy, khi hàm lượng xi măng dao động trong khoảng 280 – 450 kg/m³ của hỗn hợp bê tông, thì độ gia tăng nhiệt độ lớn nhất là 39.86°C và độ gia tăng chênh lệch nhiệt độ lớn nhất là 27.6°C (so sánh Hình 1.5 với Hình 1.6 và Hình 1.7 với Hình 1.8). Ngược lại, nhiệt độ ban đầu của hỗn hợp bê tông thay đổi trong khoảng 15 - 30°C chỉ góp phần tạo nên sự gia tăng nhiệt độ lớn nhất là 10.2°C và độ gia tăng chênh lệch nhiệt độ lớn nhất là 6.2°C (so sánh Hình 1.5 với Hình 1.7 và Hình 1.6 với Hình 1.8).
Kết quả của chương trình phân tích nhiệt bằng phương pháp phần tử hữu hạn dựa trên phần mềm - Midas Civil cho thấy nhiệt độ tối đa và chênh lệch nhiệt độ tối đa tương ứng với hàm lượng xi măng và nhiệt độ ban đầu có thể được tóm tắt trong Bảng 1.3. Sau đó, sử dụng phương pháp bình phương tối thiểu để xác định các hệ số trong phương trình (3), ta thu được các mô hình toán học dự đoán nhiệt độ tối đa và chênh lệch nhiệt độ tối đa trong khối bê tông được chỉ ra bởi phưởng trình (5), (6):
Tmax = 69.88 + 19.70x1 + 4.87x2 (5)
DeltaTmax = 33.06 + 13.35x1 + 2.65x2 (6)
Kết quả thu được ở phưởng trình (5), (6) cho thấy tất cả các yếu tố trên có tác động khá lớn đến nhiệt độ cực đại và chênh lệch nhiệt độ cực đại của khối bê tông. Nhiệt độ và chênh lệch nhiệt độ chủ yếu phụ thuộc trên các thừa số x1 (X1). Bên cạnh đó, Hình 1.9 và Hình 1.10 cho phép nhanh chóng xác định nhiệt độ cực đại (Tmax) và chênh lệch nhiệt độ cực đại (DeltaTmax) trong thể bê tông khối lớn, tại đó các thông số về hàm lượng xi măng và nhiệt độ ban đầu thay đổi trong phạm vi như đã đề cập trong Bảng 1.2.
Kiểm chứng mô hình toán học thu được: Trường hợp sử dụng hàm lượng xi măng 365kg/m³ và nhiệt độ ban đầu của hỗn hợp bê tông là 22.5°C (x1=0, x2=0) để xác định nhiệt độ lớn nhất và chênh lệch nhiệt độ lớn nhất trong khối bê tông bằng phương pháp phần tử hữu hạn sử dụng phần mềm Midas Civil. Giá trị thu được của nhiệt độ tối đa Tmax = 69.59°C và chênh lệch nhiệt độ tối đa DeltaTmax = 33.5°C sau 72 giờ kể từ khi bắt đầu xây dựng được thể hiện trong Hình 1.11.
(x1=0, x2=0 hoặc X1 = 365kg/m³, X2 = 22.5°C) Hình 1.11 cho thấy nhiệt độ tối đa trong khối bê tông Tmax = 69.59°C và chênh lệch nhiệt độ tối đa DeltaTmax = 33.5°C sau 72 giờ. Với hàm lượng xi măng 365kg/m³ và nhiệt độ ban đầu của hỗn hợp bê tông là 22.5°C(x1=0, x2=0) thay vào phương trình toán học(5), (6) thu được ở trên thì nhiệt độ tối đa Tmax = 69.88°C và chênh lệch nhiệt độ tối đa DeltaTmax = 33.06°C.
Sai số tương đối của nhiệt độ tối đa là 0.4 % và chênh lệch nhiệt độ tối đa là 1.3% giữa kết quả thu được từ phương trình toán học và kết quả thu được từ phân tích mô phỏng số theo phương pháp phần tử hữu hạn với Midas Civil mang lại sự đáng tin cậy về độ chính xác của kết quả mô hình toán học thu được.
4. Kết luận
Dựa trên kết quả nghiên cứu, có thể rút ra các kết luận sau:
- Phương pháp quy hoạch thí nghiệm sử dụng trong mô hình phản ánh mối tương quan và ảnh hưởng giữa hàm lượng xi măng và nhiệt độ ban đầu của bê tông đến sự phân bố nhiệt độ và độ chênh nhiệt độ lớn nhất trong thân kết cấu bê tông khối lớn tuổi đầu.
- Hàm toán học Tmax và DeltaTmax có thể được sử dụng để tính toán nhiệt độ tối đa và chênh lệch nhiệt độ tối đa trong thân bê tông khối lớn với hàm lượng xi măng và nhiệt độ ban đầu của hỗn hợp bê tông thay đổi trong khoảng 280 - 450kg/m³ bê tông và 15 - 30°C tương ứng.
- Hàm lượng xi măng đóng vai trò quyết định trong việc tạo ra nhiệt độ cực đại và chênh lệch nhiệt độ cực đại trong thân bê tông khối lớn khi so sánh với nhiệt độ ban đầu của hỗn hợp bê tông. Do đó, cần xem xét cẩn thận hàm lượng xi măng trong hỗn hợp bê tông khi kiểm soát nhiệt độ tối đa trong kết cấu bê tông khối lớn.
Tài liệu tham khảo
1. American Concrete Institute (ACI) (1996), ACI 207.1R-96 -Mass Concrete.
2. Malkawi, A.H., Mutasher, S.A., Qiu, T.J. (2003), "Thermal-structural modeling and temperature control of roller compacted concrete gravity dam", J Perform. Constr. Facilities, 17(4), tr. 177-187. doi: 10.1061/(ASCE)0887-3828(2003)17:4(177).
3. Nguyễn Tiến Đích (2010), Công tác bê tông trong điều kiện khí hậu nóng ẩmViệt Nam, NXB Xây Dựng, Hà Nội.
4. Adler Y P Markova Е V Granovsky Y V 1976 Experiment planning in search of optimum conditions М.: Nauka p. 70-92
5. Toan, L.Q, Te, V.T, Hung, V.H (2015), "Additional properties to perfect temperature and software ansys thermal stresses of the rcc dam in Vietnam", J. Water Res. and Environ. n. Sci., 50, tr. 9-15.
6. Vũ Chí Công, Hồ Ngọc Khoa, Lê Văn Minh (2022), "So sánh chỉ số nứt nhiệt được xác định bằng 2 phương pháp: Đánh giá đơn giản và phần tử hữu hạn của cống hộp bê tông cốt thép", Tạp chí Khoa học công nghệ xây dựng, (1).
7. Vũ Chí Công, Lê Văn Minh, Hồ Ngọc Khoa (2023), "Phân tích xác suất nứt do nhiệt của kết cấu trụ cầu trong quá trình nhiệt thủy hóa xi măng bằng mô phỏng số", Tạp chí Vật liệu vàxây dựng, (13).
8. J.E Akin (1994), Finite Element for Analysis and Design, Academic Press.
9. P. P. Bamforth, D.Chisholm, J.Gibbs, T.Harrison (2008), Properties of Concrete for use in Eurocode 2, The Concrete centre.
10. B. Gebhart (1993), Heat Condtion and Mass Diffusion, McGraw-Hill.
11. Japan Concrete Institute (2011), "Guideline for control of cracking of mass concrete".
12. Lam, T.V., Bulgakov, B.I., Aleksandrova, O.V., Larsen, O.A., Anh, P.N (2018 ), "Effect of rice husk ash and fly ash on the compressive strength of high performance concrete", E3S Web of Conf. 33, 02030. doi: 10.1051/e3sconf/20183302030.
VLXD.org (TH/ TC Xây dựng)




 Sitemap
Sitemap Thành viên
Thành viên