1. Mở đầu
Mặt nón là một mặt cong hình học 3 chiều được công nhận rộng rãi và hiện diện nhiều trong đời sống hàng ngày, rất nhiều vật dụng có hình dạng của mặt nón từ chiếc nón đội đầu đến các món đồ nội thất như: đèn, bàn, ghế, bình hoa... hình mặt nón. Mặt nón có hình dạng linh hoạt với nhiều ứng dụng trong toán học, vật lý, kỹ thuật và nghệ thuật, đặc biệt trong lĩnh vực kiến trúc và xây dựng. Mặt nón đã được sử dụng trong suốt chiều dài lịch sử theo nhiều cách khác nhau và sự phổ biến lâu dài của nó là minh chứng cho vẻ đẹp và sự tiện ích vượt thời gian của mặt nón.
2. Khái niệm về mặt nón
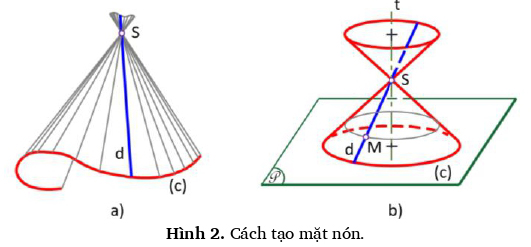
Mặt nón là mặt tạo bởi một đường thẳng chuyển động (gọi là đường sinh) đi qua một điểm cố định (gọi là đỉnh của mặt nón) và tựa trên một đường cong (gọi là đường chuẩn của mặt nón). Hình 2.a biểu diễn mặt nón được tạo bởi đường sinh d chuyển động đi qua đỉnh S cố định và tựa trên đường cong (c). Trường hợp đặc biệt, khi quay đường thẳng d quanh một trục t cắt nó tại S ta có nón tròn xoay như Hình 2.b. Mỗi điểm trên d vạch thành một đường tròn (gọi là đường tròn vỹ tuyến). Nón tròn xoay có đường chuẩn (c) là đường tròn, mặt phẳng chuẩn P (mặt phẳng chứa đường chuẩn) vuông góc với trục quay t. [1] [2] [3]
3. Biểu diễn mặt nón trên hình chiếu thẳng góc
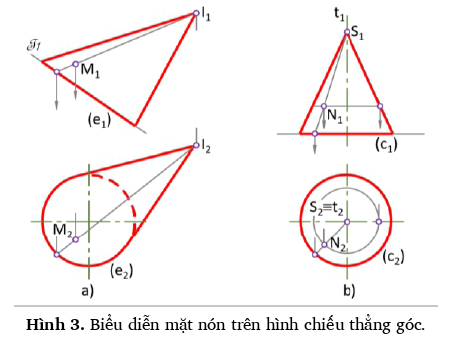
Để biểu diễn mặt nón cần:
- Biểu diễn các yếu tố đủ để xác định nón: đường chuẩn, đỉnh, trục (nếu là nón tròn xoay);
- Vẽ các đường bao quanh hình chiếu của mặt;
- Xác định được một điểm bất kì của mặt.
Hình 3.a biểu diễn hai hình chiếu thẳng góc của nón đỉnh I, đường chuẩn là elip (e) thuộc mặt phẳng chuẩn T chiếu đứng, hình chiếu bằng của đường chuẩn elip (e) suy biến thành đường tròn. Để xác định hình chiếu bằng M2 của điểm M thuộc nón (biết M1 thấy), cần gắn M vào một đường sinh của nón (đường sinh của nón luôn đi qua đỉnh nón và một điểm trên đường chuẩn).
Trong thực tế thường gặp mặt nón ở dạng nón tròn xoay. Hình 3.b biểu diễn hai hình chiếu thẳng góc của nón tròn xoay đỉnh S, đường chuẩn (c) thuộc mặt phẳng hình chiếu bằng, trục quay t vuông góc với mặt phẳng hình chiếu bằng, đi qua đỉnh S và tâm của đường chuẩn (c). Vì nón tròn xoay vừa là một mặt kẻ, vừa là một mặt tròn xoay nên để xác định hình chiếu bằng N2 của điểm N thuộc nón (biết N1 thấy) có 2 cách:
- Cách 1: gắn N vào một đường tròn vỹ tuyến của nón (đường tròn này nằm trong mặt phẳng bằng nên hình chiếu bằng của nó là một đường tròn - lặp lại hình dạng của đường chuẩn);
- Cách 2: gắn N vào một đường sinh của nón. [1] [2]
4. Các dạng thiết diện của mặt nón
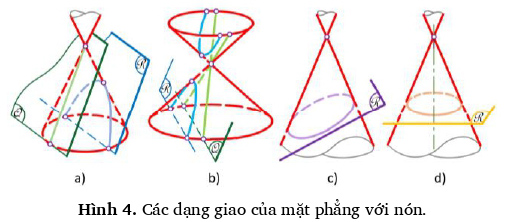
Nói chung giao của mặt phẳng với mặt cong đại số bậc n là một đường cong đại số bậc n. Xét mặt nón bậc 2 (có đường chuẩn là một đường cong bậc 2 như: đường tròn, elip, parabol, hyperbol), giao của mặt phẳng với mặt nón có thể là:
- Một đường sinh khi mặt phẳng tiếp xúc với mặt nón (Hình 4.a - mặt phẳng Q cắt nón giao là một đường sinh - đường tiếp xúc của mặt phẳng Q với mặt nón);
- Hai đường sinh khi mặt phẳng đi qua đỉnh nón và cắt đáy nón ở hai điểm (Hình 4.b - mặt phẳng Q cắt nón giao là hai đường sinh);
- Elip khi mặt phẳng cắt mọi đường sinh của nón (Hình 4.c - mặt phẳng R cắt mọi đường sinh của nón giao là elip);
- Parabol khi mặt phẳng song song với chỉ một đường sinh của nón (Hình 4.a - mặt phẳng R cắt nón giao là parabol);
- Hyperbol khi mặt phẳng song song với hai đường sinh của nón (Hình 4.b - mặt phẳng R cắt nón giao là hyperbol).
- Trường hợp đặc biệt: mặt phẳng vuông góc với trục của nón tròn xoay cắt nón tròn xoay giao là đường tròn vỹ tuyến (Hình 4.d - mặt phẳng R cắt nón tròn xoay giao là đường tròn vỹ tuyến). [1] [2]
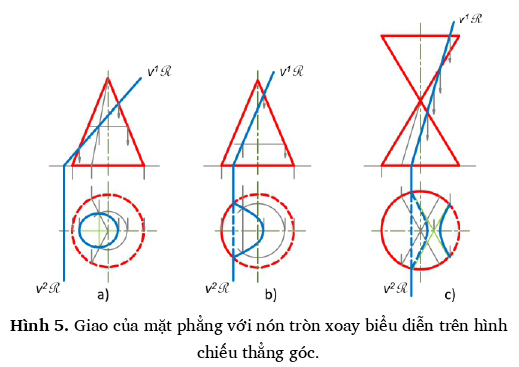
Để vẽ giao của một mặt phẳng với một mặt nón thường tìm nhiều điểm chung của chúng. Mỗi điểm chung là giao điểm của một đường sinh thẳng của mặt nón với mặt phẳng đã cho. Vấn đề quy về cách vẽ giao điểm của một đường thẳng với một mặt phẳng. Ngoài ra, cần tìm các yếu tố xác định giao như: tâm, trục, đường kính liên hợp, tiếp tuyến, tiệm cận. Hình 5.a biểu diễn giao của mặt phẳng chiếu đứng R với mặt nón tròn xoay, mặt phẳng R cắt qua mọi đường sinh của nón - giao tuyến là elip (hình chiếu đứng elip giao suy biến thành đoạn thẳng trùng với v1R, hình chiếu bằng là elip). Hình 5.b biểu diễn giao của mặt phẳng chiếu đứng R với mặt nón tròn xoay, mặt phẳng R song song với một đường sinh của nón - giao tuyến là parabol (hình chiếu đứng parabol giao suy biến thành đoạn thẳng trùng với v1R, hình chiếu bằng là parabol). Hình 5.c biểu diễn giao của mặt phẳng chiếu đứng R với mặt nón tròn xoay, mặt phẳng R song song với hai đường sinh của nón -giao tuyến là hyperbol (hình chiếu đứng hyperbol giao suy biến thành đoạn thẳng trùng với v1R, hình chiếu bằng là hyperbol).
5. Ứng dụng mặt nón trong thiết kế kiến trúc
Mái hình nón thường thấy trên đỉnh tháp trong các pháo đài và lâu đài của các thị trấn thời trung cổ. Mặt mái hình nón có thể nằm trực tiếp trên bức tường bên ngoài của tháp hoặc đôi khi có phần nhô ra ngoài để tạo thành mái hiên. Những mái nhà hình nón như vậy thường được xây dựng bằng cách sử dụng một kết cấu đỡ khung gô phủ đá phiến, hoặc được làm bằng gạch xây. Mái hình nón được sử dụng rộng rãi trong kiến trúc nhà thờ Armenia và Gruzia và cũng được sử dụng nhiều ở các vùng nông thôn cho các tòa nhà hình tròn hoặc hình vuông nhỏ.

Cấu trúc nón cũng được tìm thấy nhiều ở các công trình dạng tháp nước: Tháp nước Benbecula ở Balivanich (1970), Tháp nước Gemozac ở Pháp (1997), Tháp nước M11 ở Anh (1993), Tháp nước Midrand ở Nam Phi (1996), Tháp nước Tonwell ở Anh (1964). Ngày nay, một số tháp nước lâu đời đã được chuyển đổi mục đích sử dụng thành khu phức hợp nhà hàng, tháp quan sát, đài phát thanh địa phương, trạm điện thoai công cộng, căn hộ nghỉ dưỡng... dù với mục đích sử dụng nào thì đây đều là những minh chứng lịch sử, những công trình mang tính biểu tượng với hình ảnh đặc trưng như một cột mốc đánh dấu cho một vùng đất.

Mặt nón đã được sử dụng trong nhiều loại công trình chức năng khác như bảo tàng, thư viện, khách sạn, nhà ở...
Bảo tàng Solomon Robert Guggenheim là tác phẩm cuối cùng trong số 600 công trình đã xây dựng của kiến trúc sư Frank Lloyd Wright, được hoàn thành vào năm 1959 tại Thành phố New York (Hoa Kỳ). Công trình có khu vực bảo tàng chính mang hình dáng một mặt nón cụt dưới nhỏ, trên to. Sau khi đi thang máy lên trên, người xem theo một sàn nghiêng thoải dần, xoắn ốc xuống dần tới tầng một. Đó là một không gian bảo tàng kiểu mới, người tham quan đứng ở vị trí nào ở các tầng cũng có thể chiêm ngưỡng cây xanh và trang trí ở tầng một.

Thư viện TU Delft là thư viện chính của Đại học Công nghệ Delft (TU Delft) nằm ở Delft, Hà Lan. Nó được thiết kế bởi công ty kiến trúc Mecanoo của Hà Lan và được xây dựng vào năm 1997. Đây là thư viện khoa học kỹ thuật lớn nhất ở Hà Lan. Thư viện nằm một phần dưới lòng đất với mặt phẳng dốc 15% và mái nhà phủ đầy cỏ xanh trên đỉnh. Nhô ra từ ngọn đồi nhân tạo có một hình nón bằng thép cao 40 mét hoạt động như một nguồn ánh sáng ban ngày và có ý nghĩa tượng trưng cho kỹ thuật.

Hội quán PokoPoko là trung tâm hoạt động và hội quán dành cho gia đình ở Nhật. PokoPoko được đặt tên theo từ tượng thanh tiếng Nhật “poko poko”, có nghĩa là nhô ra ngoài, và giống như một địa danh dân gian. Công trình có thể nhìn thấy từ xa với ba mái nhà hình nón lấp ló một cách bí ẩn từ khu rừng xung quanh của Cao nguyên Nasu. Nhìn gần, ba mái nhà của PokoPoko cho thấy chúng dính liền với nhau thành một tòa nhà duy nhất, với môi hình nón khổng lồ có hình dạng khác nhau và không đối xứng một cách tinh nghịch. PokoPoko phản ánh mong muốn sống chậm lại, thích ở bên gia đình, khám phá môi trường địa phương và tìm thấy niềm vui trong những điều đơn giản hơn trong cuộc sống. Tính thẩm mỹ của nó là nhịp nhàng và tự nhiên, những hình nón lấy cảm hứng từ túp lều được xây dựng từ những mảnh gô thông và gô có nguồn gốc địa phương.

Hình khối kiến trúc càng cấu tạo bởi các mặt hình học đơn giản bao nhiêu thì hiệu quả nghệ thuật mang đến lại càng mạnh mẽ và rõ ràng bấy nhiêu. Trong thiên nhiên ít khi gặp các hình thức hình học đơn giản vì thế việc vận dụng các mặt hình học này sẽ mang lại ấn tượng về nghệ thuật tương phản đối với môi trường xung quanh. Và mặt nón khi sử dụng hình dạng nguyên bản của nó có thể tạo được hiệu ứng thị giác mạnh mẽ với nguyên lý này. Ngoài ra, cũng có thể cắt ghép mặt nón hay phối hợp cùng các mặt khác để tạo nên các hình thức kiến trúc đa dạng hơn. Để ghép các mảnh mặt bậc hai, người ta thường dùng các định lý về giao tuyến các mặt bậc hai trong các trường hợp đặc biệt. Bình thường giao của hai mặt bậc hai là một đường cong bậc bốn, nhưng có một số trường hợp đặc biệt, đường bậc bốn suy biến thành đường bậc hai (đó là hai đường cong phẳng). Điều này cho phép ta có thể ghép các mảnh mặt lại một cách đơn giản. Dựa trên các dạng thiết diện đã biết, ta có thể chủ động cắt mặt Nón theo các thiết diện mong muốn và ghép lại với nhau. Việc ghép mặt được thực hiện dê dàng nhất trong trường hợp thiết diện có dạng tam giác (dạng giao hai đường sinh) và tròn.
6. Kết luận
Các mặt hình học từ đơn giản đến phức tạp được ứng dụng rất nhiều trong thiết kế kiến trúc, xây dựng và tạo hình các sản phẩm, đồ dùng phục vụ đời sống. Hình học giúp người thiết kế trình bày và hiện thực hóa các ý tưởng của mình. Hình học xác định không gian và tạo nên dấu ấn cho công trình. Trong quá trình thiết kế và xây dựng, việc ứng dụng các mặt hình học không chỉ đòi hỏi đáp ứng về mặt thẩm mỹ mà còn cần đáp ứng các tiêu chí về khả năng xây dựng dê dàng và hiệu quả kinh tế.
Mặt nón là một mặt cong đã được sử dụng rộng rãi trong kiến trúc và xây dựng từ xưa đến nay, từ được ứng dụng làm các chi tiết trang trí đến làm hình khối chính cho công trình. Là một trong những hình thức mang tính biểu tượng nhất, mặt nón đã được tìm thấy trong các tòa nhà và nền văn hóa trên khắp thế giới. Mặt nón không chỉ mang vẻ đẹp của mặt cong mà còn có khả năng chịu lực tốt và xây dựng dê dàng từ các dầm thẳng. Người thiết kế vừa có thể ứng dụng mặt nón ở dạng nguyên bản, vừa có thể cắt ghép nhiều mặt nón với nhau hoặc với các mặt hình học khác tùy vào khả năng sáng tạo của mình để tạo nên những hình thức kiến trúc mới mẻ và độc đáo.
Tài liệu tham khảo
[1]. Nguyên Đình Điện, Đỗ Mạnh Môn (2008): Hình học họa hình Tập 1. NXB Giáo dục, Hà Nội.
[2]. Nguyên Thị Minh Thùy, Nguyên Xuân Hoan, Nguyên Thị Chính, Phan Thị Hoàng Yến, Phạm Thị Thanh Vân, Nguyên Thị Chung Hiếu, Nguyên Văn Tuấn (2020): Bài giảng Hình học họa hình. NXB Dân trí, Hà Nội.
[3]. Đoàn Như Kim (2005): Một số khái niệm về hình học trong kiến trúc. NXB Xây dựng, Hà Nội.
[4]. Nguồn internet: //en.wikipedia.org; //www.pinterest.com; //architizer.com; //www.flickr.com; //www.dezeen.com; //www.archdaily.com
VLXD.org (TH/ JOMC)
 Sitemap
Sitemap Thành viên
Thành viên 























































